最近SC AI做得差不多了，忽然想到应该写一写关于ANN和GA的科普文章呢，毕竟自己学习只是一部分，跟大家分享也很重要嘛。自己叙述一遍的话，也能考察自己掌握的程度。

ANN, artificial neural network, 即人工神经网络，是机器学习的一种模型。我学习这个其实也是读教科书，用的是卡内基梅隆大学那本machine learning。

所以先说说机器学习吧。机器学习的基本思想就是不通过编程来让计算机完全遵守人指定的死板的流程，而是通过定义一个可学习的模型，之后向这个模型不断添加<问题，答案>这样的对（正式名称是<输入样例，目标输出>），来让计算机通过经验判断下一次接收到问题的时候，应该做出怎样的回答。

其解决方案就是根据每一次的计算机回答和人指定的标准答案进行对照，假如相符，则给予鼓励；假如不相符，则给予批评（即正激励和负激励）。通过不断的训练引导计算机逐渐获得对相关知识的理解。

人工神经网络是机器学习的一个解决方案，即采取仿生的神经元结构来对计算机进行训练。由于人的神经元的复杂性，目前用于计算机研究的神经网络通常采取的是一种简化模型。他令神经元有一个输出和多个输入。神经元通过对所有的输入进行加权求和计算出结果，并以这个结果作为输出（可以想象出来，训练一个神经网络，其实就是训练他使得每一个神经元都得到正确的权值组合）。为了保持简洁性，每个神经元的输入和输出都最好保持在0～1之间。于是这里采取了一个挤压函数，将实数域映射到0~1之间的一个小集合上。通常采用的挤压函数是sigmoid函数，sigmoid(x)=1/(1+exp(-x))。当然也可使用其他有类似特点的函数变体啦。定义好神经元之后，须将神经元根据问题需要构造成神经网络。目前业界通用的较为稳定的神经网络是单向无环的结构。往往采取三层。

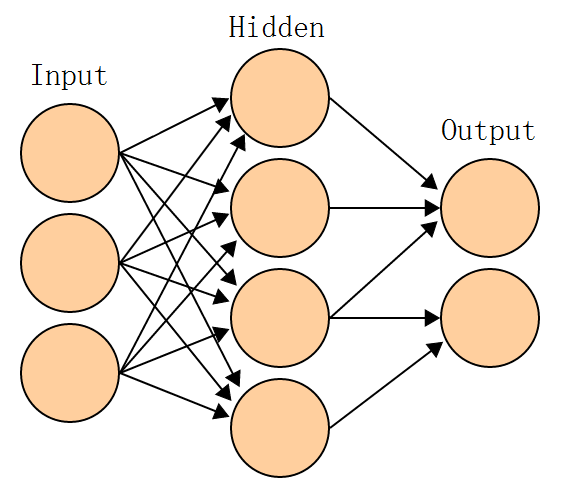
第一层是输入层，根据需要，要把问题转换为一个编码，并依次作为输入给各个输入曾神经元赋值。例如，用于人脸识别的神经网络，可采取一个人脸照片的32×32的缩略图作为输入，这样的话就需要1024个输入，每个输入是0~255的像素灰度信息。有比如要从今天的天气情况推算明天的天气情况（当然实际是不可行的。。），可将想要考虑的所有天气特征依次作为输入，并传输给各个神经元。
第二层是隐藏层，它的作用是增加神经网络的复杂度，从而使神经网络可以表达更复杂的函数逻辑。已经证明，任意函数可被三层单馈神经网络（一个输入层，两个隐藏层和一个输出层）以任意精度逼近。但是，更复杂的函数就需要更多的神经单元来表征。由于我们在实现神经网络之前，往往并不能确定问题的复杂度，所以隐藏层采用的神经元数量往往是要靠经验得出的。当然也有一些动态修正的方法可以在训练的过程中增加或减少隐藏层的单元数量。
第三层是输出层，输出单元一般不使用挤压函数处理，而是让他输出线性的数据，以便同实际问题相联系。输出层同样要根据实际问题来编码。例如在人脸识别的应用中，可采取两个输出，一个表示“是人脸”，一个表示“不是人脸”，这里输出还是在0～1之间的。可采取一个阈值来确定真假，例如用>0.7表示真，<0.3表示假，之间是模糊状态。之所以采用两个输出而不是自然想到的一个，是为了稳定性。当两个神经元的输出相符时（例如“是人脸”输出0.9,“不是人脸”输出0.1），可认为模型正确得出结论；而当两个输出不符时（例如均输出0.7），则表示模型无法准确判断。

建立好模型之后就是训练了。这里采取的方法称作“梯度下降的反向传播算法”。之所以称作梯度下降，是说根据人确定的正确答案和计算机通过神经网络给出的答案之间应该会有一个差距。将这个差应用到得出这个结果的输出层上，就能得出输出层的每一个权值应该向哪个方向调整。注意到神经元输出是输入的加权和，所以权值较大的那个分量对于结果的贡献越显著，因此在训练时对他的反馈也应该相应得更明显。数学上采用方差对于权值的函数形成曲面的梯度来描写这个特征。沿着梯度下降到曲面的最小值（有时只能达到局部极小值），就是训练成功了。由于梯度从概念上说是一个无穷小增量，这里只能定义一个较小的“学习速率” η 来作为每次修正权值的增量基准。η取得太大会导致无法达到曲面的最小值（总是越过他），而太小则会导致训练的迭代次数过多，同时也会使得只能达到局部极小值（无法越过局部最小值的谷底）的问题变得严重，因此也有采用变化的η值，例如逐渐减小的η（加快训练速度），又或者带有冲量的η（越过局部最小值的谷底）。这里它的取值变成了一个复杂的研究课题这里不表了。
这就解释了什么叫做“梯度下降”，再来解释反向传播。前面说到根据输出o和标准答案t可以得到一个方差，从而修正输出单元的权值，但如何修正隐藏单元的权值呢（输入单元只有一个输入，因此没有权值也无需训练）？这就是要用到反向传播的地方。既然已经得出了修正后的输出层权值，就又可将输出层的每一个输入（即隐藏层的每一个输出）的实际值和目标值，将修正“反馈”到上一层去。当然仍然需按照每一个权值贡献不同按比例反馈。反馈之后即可得到这层单元的“目标值”了，在用这个目标值在这一层做梯度下降进行训练，这样做一直反馈到输入层为止。
总之假如能够训练使得函数达到最小值，就表示训练成功了。因为它的含义是合适的权值取值，使得模型的输出结果o和标准答案t之间的方差最小。注意由于输出单元往往不止一个所以这里o和t都是向量。方差指的是每一个单元的输出方差再求和。

好吧这些就是理论讲解啦。当然实际应用的时候对于不同的问题会有不同的变形。无论是学习速率，挤压函数，还是权值的梯度下降算法，都可以有这样或那样的改变。这些就是一方面凭经验，另一方面也靠创造性的想象力和“尝试-失败-尝试”的方法来验证啦～

链接：
维基百科-人工神经网络 http://en.wikipedia.org/wiki/Artificial_neural_network
维基百科-反向传播算法 http://en.wikipedia.org/wiki/Backpropagation
维基百科-梯度下降算法 http://en.wikipedia.org/wiki/Gradient_descent
维基百科-机器学习 http://en.wikipedia.org/wiki/Machine_learning
图书 《机器学习》 http://www.cs.cmu.edu/~tom/mlbook.html