最近朋友跟我讨论了一个类型的旅行商问题。原版的旅行商问题是说，给定一个图，给定起点和终点，求不重复经过任何节点的最短路径，遍历全部节点。而他的问题是，仍然不许重复经过任何节点，但是不要求路径遍历全部节点，而是遍历某一个给定的关键点集，求最短路径。问题里面对图没有做任何限制，图可能包含数千节点，不过关键点集是充分小的，比如只有5个关键点，这样。

一开始我没听清楚题目，以为这个问题跟斯坦纳树有什么关系。（所以才会写了上面一篇note。。）不过后来知道不许重复经过节点，那么这种想法就没有用了。

不过既然关键点集充分小，求的又是路径，那么几个关键点必然只能依次经过。可以尝试所有关键点的排列，依次求最短路径。比如说5个关键点，也只需要算120次。还算可以接受吧。并且假如采取分支定界，其实还是可以减去很多分支的。当然可以构造出几个关键点无论怎么排列，路径都等长的情况。比如所有两两点间都有路径长度为1的任何图，都是这样。。。不过假如是工程上使用的话，可能还有其他办法可以提前退出，比如求出“足够好”的解，或者算了很长时间，一直没有找到更好的解，之类的。。这个就可以根据需求而定了。

不过朋友比较担心的是割点的问题。割点是说，一旦去掉这个点，则图会被拆成两个独立的联通分量。就是说从图的某些点出发，永远也无法到达图的另外一些点了。。之所以担心这类点，是怕一旦算法的前面走过了这类点，那么由于存在不许重复任何节点的限制，可能导致某些点无法经过了。那么这个割点至少有两种情况。就是这个割点会导致关键点被割掉，或者只会导致非关键点被割掉。

导致非关键点被割掉的那种割点，可以直接收缩为一个点。因为题目并不要求遍历非关键点。并且求出的路径绝不可能进到那个割点后面去（因为1.里面没有关键点，2. 进去就出不来了）。那么至于说会导致关键点被割掉的情况呢？暂且也把他收缩为一个点吧。如果不断这样收缩，整个图就会最终退化为不含割点的图。并且最后一次收缩的割点应该不会超过两个。假如超过两个，那么这个图是无解的。因为总有一些关键点，你要经过一个割点才能进去，然后就出不来了。至于不超过两个，那是说起点和终点可以从割点经过。当然这个是欧拉说的啦。。

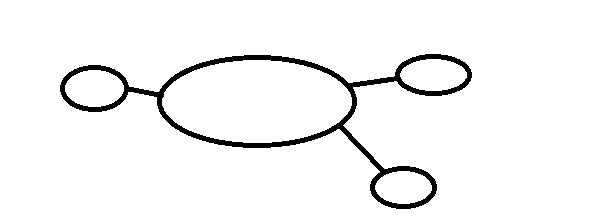
比如上面的图，每个椭圆表示里面有一坨点，并且里面的每个点都至少有两个入度。假如上图的三个小椭圆里面都有关键点，那么这个题就无解了。假如任何一个小椭圆里面没有关键点，那么就可以直接去掉。

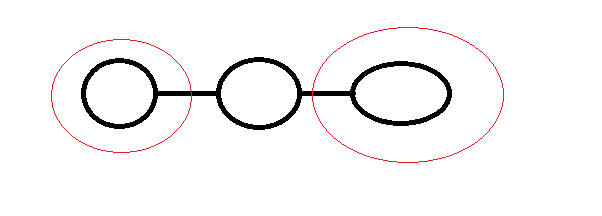最后肯定只有不超过两个小椭圆里面是有关键点的。比如上图的红色椭圆。可以暂时收缩成一个点。

所以最后一次收缩的割点，不会超过两个。

那么其实这种收缩可以重复进行，于是可以写出递归代码来解。当然现在问题就转化成，对于没有割点的情况，怎么解这个问题。

当然其实问题的难点，也正是在没有割点的情况下吧。。还是继续前面那种遍历所有关键点顺序的那个思路，这回每次需要考虑的关键点都变少了（好吧也可能没变少，至少不会变多！！）。接下来的事情可以参考旅行商问题的一般解法来求吧。。因为不是我的题目，所以没有继续去查。。同样是做个记录留下来吧。。还是方便以后捡回来。。