这个命题想了好久。实在不容易定义一个准确清晰的模型来描述这个问题。

从简单的开始吧。

首先SC地图是米字格拼成的，从每个位置向外都有八个方向。当然很传统的，每个位置都可以视为可通过或不可通过。除此之外，在可通过的位置上还有一些比如高度，是否掩护之类的一些属性需要考虑。暂时先讨论开阔地吧。

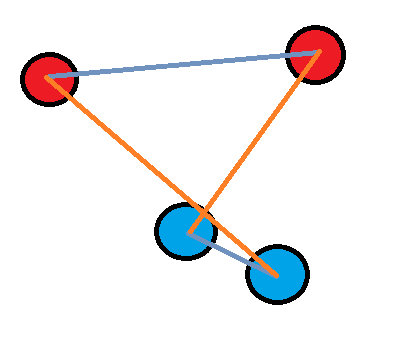
从最简单的情况开始考虑。比如红蓝两方各有2个狂徒，如何微操可以尽快消灭敌人呢？进一步简化问题，令红方谋求进攻，而蓝方决定防守。当然是将两个狂徒同时攻击对手的同一个狂徒。同时尽可能防止对手的两个狂徒攻击自己的同一个。如何做到这一点呢。假如红方在不断移动，而蓝方仅仅是站着，直到红方攻击蓝方才给予反击，那么，红方应该移动到怎样的位置时就可以决定攻击了呢？应该是红方的两个狂徒都能移动并攻击蓝方的1号狂徒，而蓝方的2号狂徒移动并加入战斗所需时间至少比1号开始同时遭受红方两个狂徒攻击晚一轮攻击所需时间。这样红方就能在攻击中占得至少一次攻击的便宜。由此看来，蓝方必须保证自己的两个狂徒之间的距离不超过红方任何狂徒到己方两个狂徒的最大值的最小值（好吧我语无伦次了）。解释一下就是红方两个狂徒到蓝方一个确定的狂徒之间的距离取最大值，而在以两个蓝方狂徒为目的地的距离之间取最小值。

显然为了做到这一点，蓝方必须移动。蓝方必须移动而保证两个狂徒间的距离没有对手到自己的距离远。这很容易做到。只需两个狂徒尽可能贴近就好了。此外当红方试图接近其中一个蓝方狂徒的时候，蓝方受到威胁的狂徒（被取了最小值的那个）向后移动绕到另一个狂徒侧面，从而使得两个距离变得尽可能相等。

假如蓝方使用这种防御方式，则红方将很难找到理想的攻击位置。但是由于蓝方为了保证距离相等必须不断移动。在移动过程中总会出现与红方距离不和谐的状态。红方只需抓住机会尽快冲上去就好了。当然蓝方鉴于此，一定不会简单的同红方对拼。而会不断后退避免冲突。无论怎样。这个最大值的最小值可以作为一个合理的AI指导原则。至于进一步的讨论要等实际测试之后再做分析了。

接下来讨论一下更多的狂徒群P的情况。想要找出一个完美的模型非常不易。可以用一条边将处于视野范围内的狂徒跟自己连起来。这样所有距离较近的狂徒就能连成一个无向图。边长表示狂徒的距离。前面说到的最大值的最小值可以用一些图论算法找出来。可是现在的问题变得非常复杂。因为之前仅考虑两个狂徒同时攻击某个单独的狂徒。而现在却需要考虑令1~n个狂徒同时攻击一个狂徒。这有n的组合种方式，还要乘以敌对狂徒的数量。这过于复杂，不可能实时计算。

采取机器学习很可能是必要的。可是如何构造决策树和估值函数却非常困扰。

现在能想到的一种简单的策略是将手下的狂徒两两结对。之后每两个一组去捕猎对手的某一个狂徒。当然过程中可以决定切换目标或者撤退。但是这种策略很可能无法发挥狂徒数量多的优势。或许可以进一步将每两组狂徒编为一个小队，每个小队去尝试捕猎对手的某2个狂徒，然后再把这两个目标分配到小组。这就形成了树状结构，像军队那样层层管理。或许这样的主意会不错。至于如何编制，以及各个级别的AI如何实现，还是等测试一段时间再总结讨论吧。